1. 跳表

节选自力扣

1.1 简述

跳表这种数据结构是由 William Pugh 发明的，是一个典型的使用空间复杂度来替换时间复杂度的数据结构，关于跳表的详细介绍可以参考论文:《Skip Lists: A Probabilistic Alternative to Balanced Trees》，论文中详细阐述了关于skiplist 查找元素、删除元素、插入元素的算法伪代码，以及时间复杂度的分析。跳表是一种随机化的数据结构，可以被看做二叉树的一个变种，它在性能上和红黑树、AVL 树不相上下，但是跳表的原理非常简单，目前在 Redis 和 LevelDB 中都有用到。跳表的期望空间复杂度为 O(n)，跳表的查询，插入和删除操作的期望时间复杂度均为 O(logn)。跳表实际为一种多层的有序链表，跳表的每一层都为一个有序链表，且满足每个位于第 i 层的节点有 p 的概率出现在第 i+1 层，其中 p 为常数。

1.2 图示

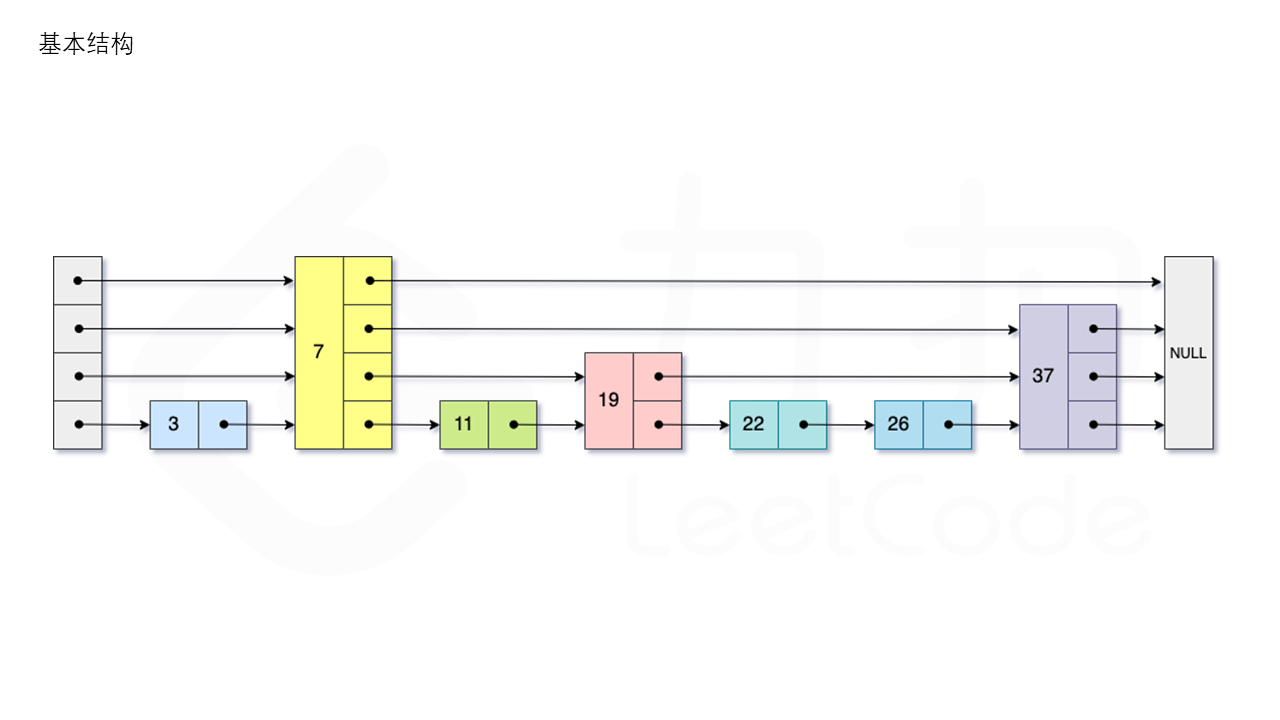
1.3 操作

1.3.1 查询

从跳表的当前的最大层数 level 层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第 1 层。此时，若第 1 层的下一个节点的值等于 target，则返回 true；反之，则返回 false。如图所示：

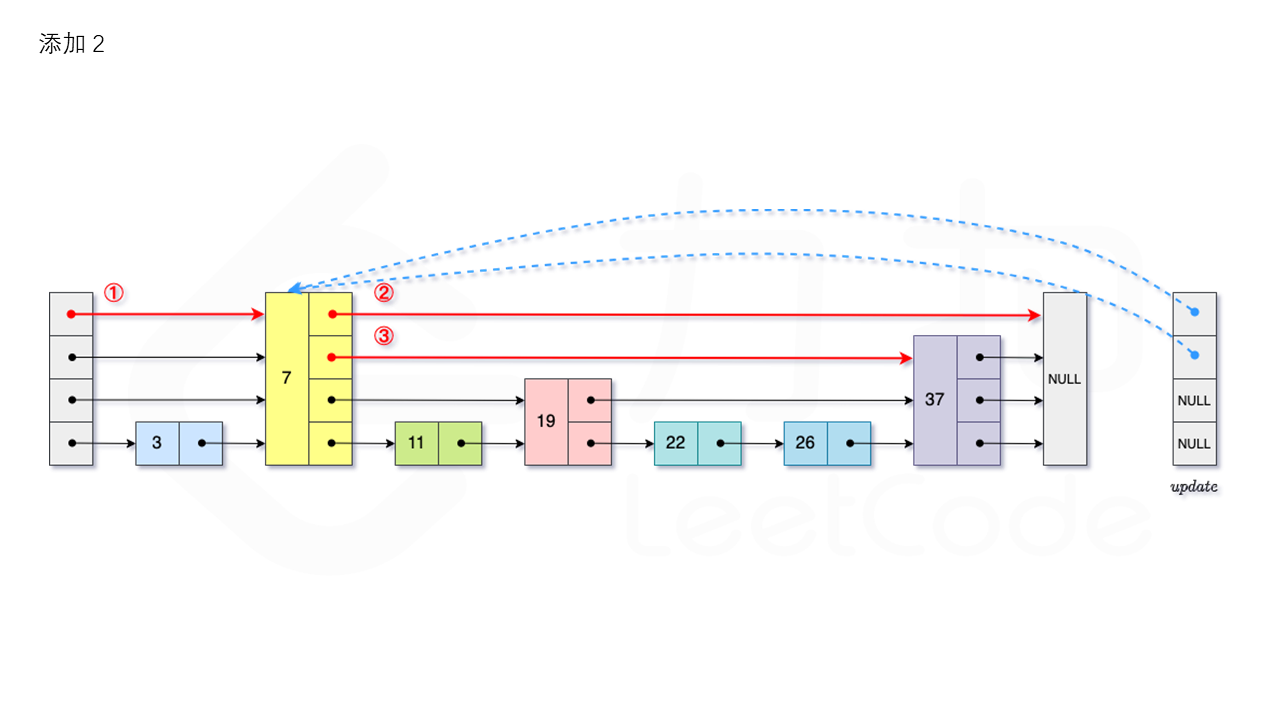
1.3.2 插入

从跳表的当前的最大层数 level 层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第 1 层。设新加入的节点为 newNode，我们需要计算出此次节点插入的层数 \textit{lv}lv，如果 level 小于 lv，则同时需要更新 level。我们用数组 update 保存每一层查找的最后一个节点，第 i 层最后的节点为update[i]。我们将 newNode 的后续节点指向 update[i] 的下一个节点，同时更新 update[i] 的后续节点为 newNode。如图所示：

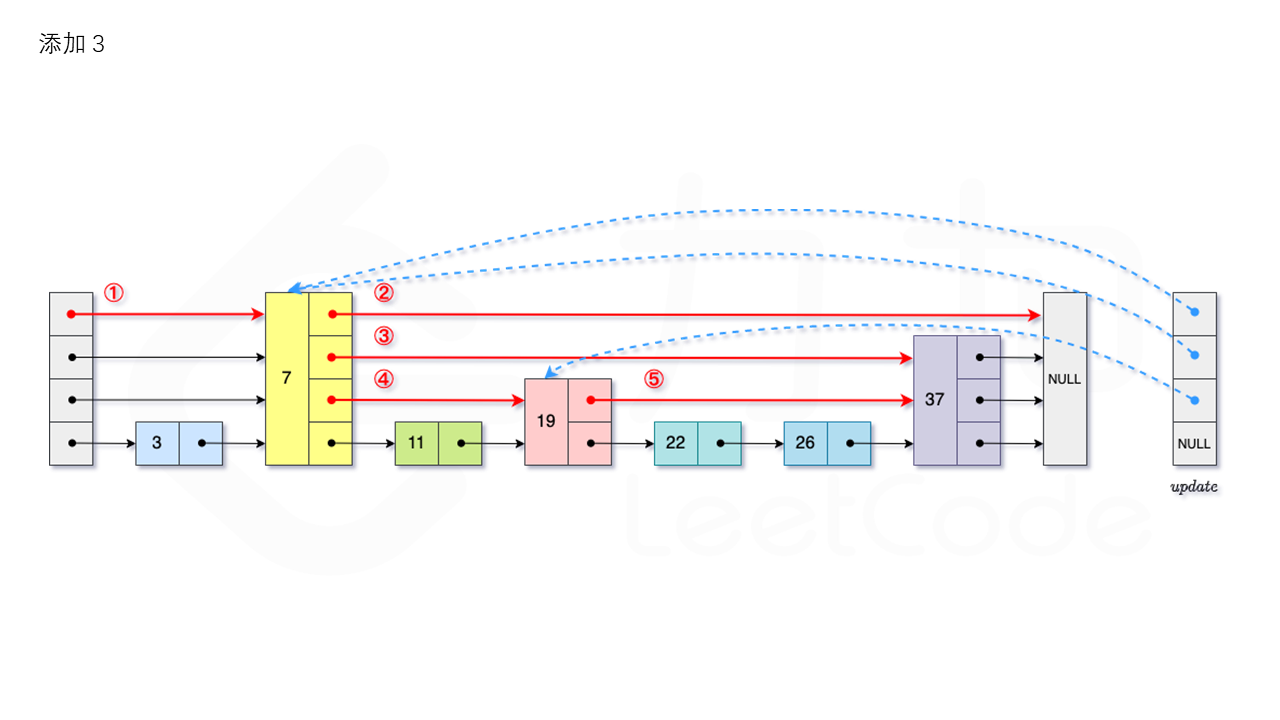
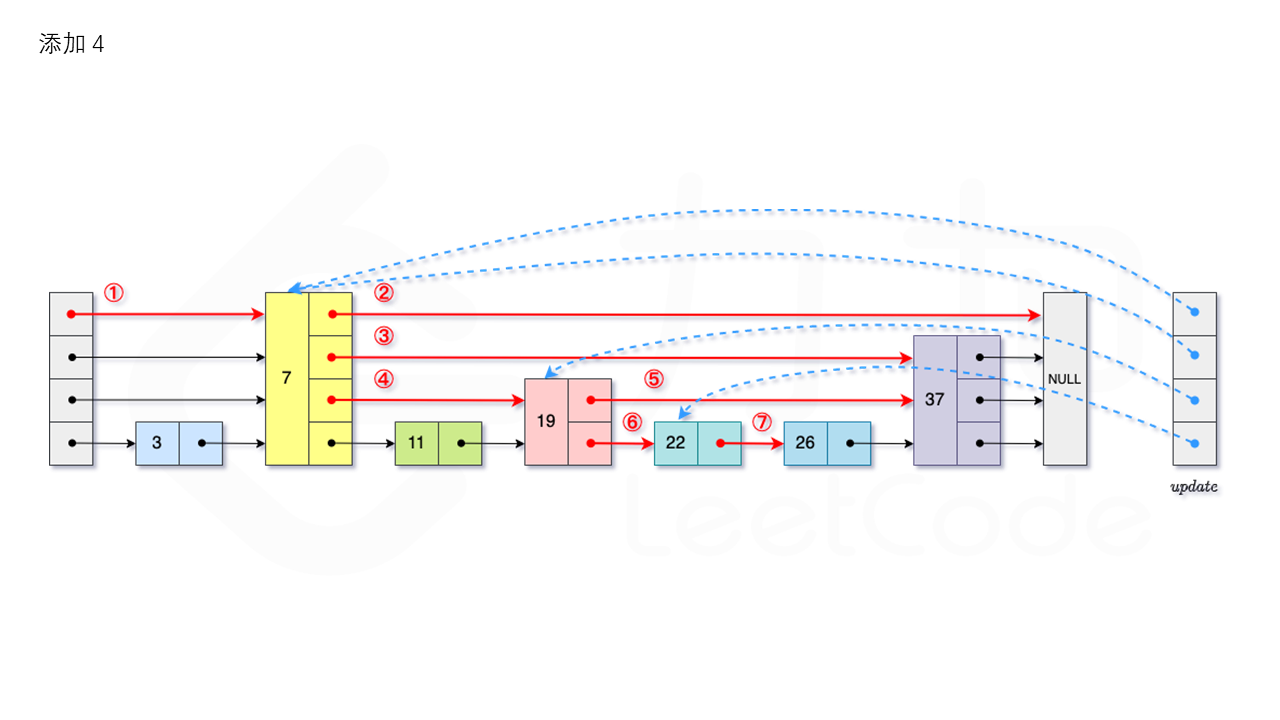
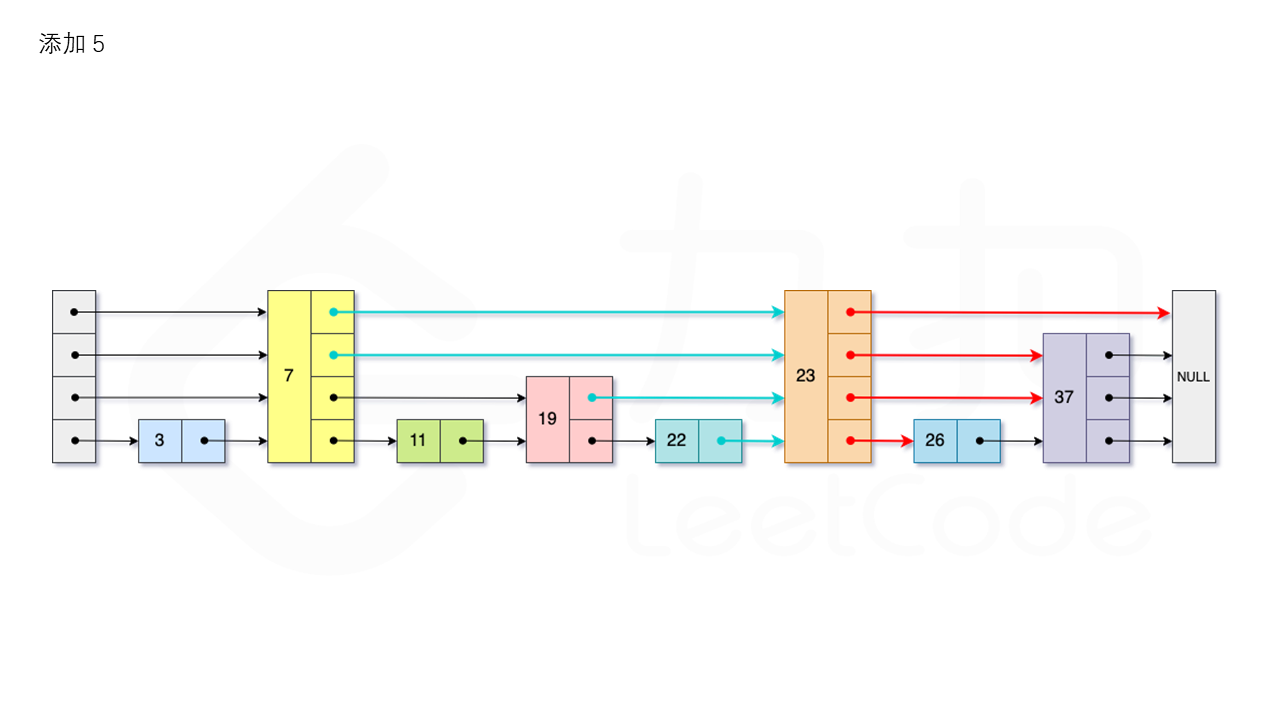
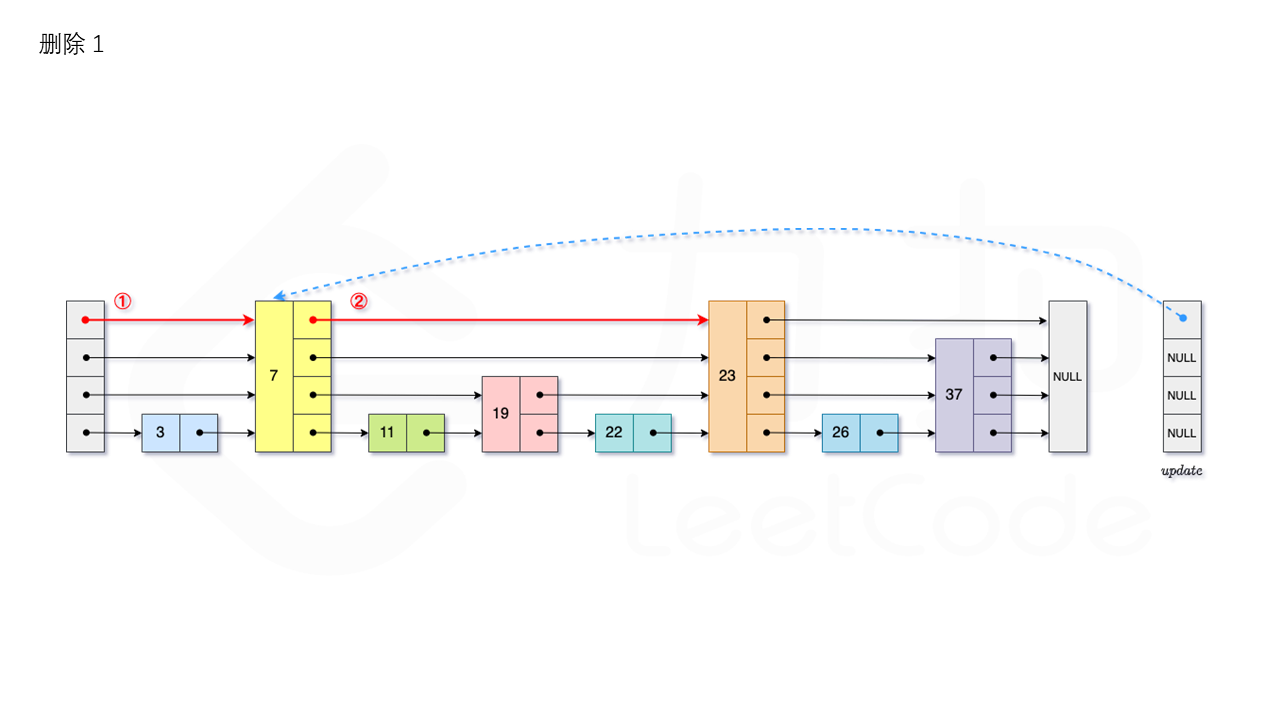
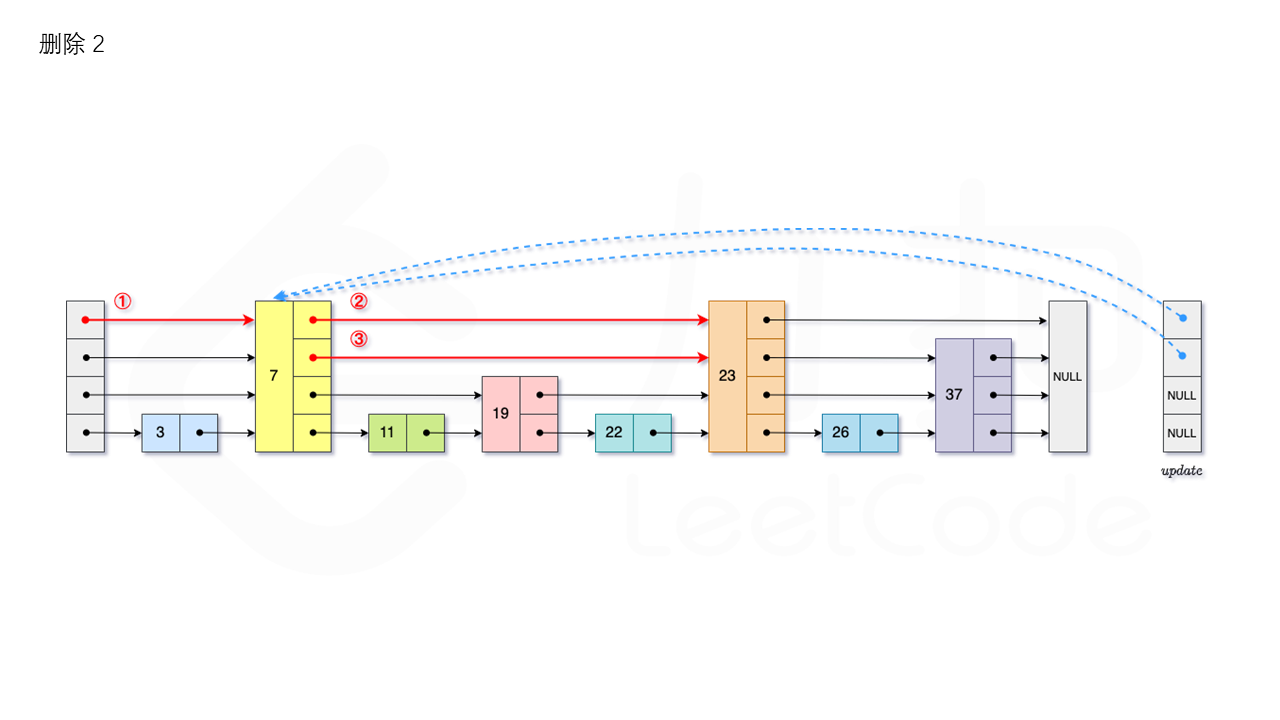
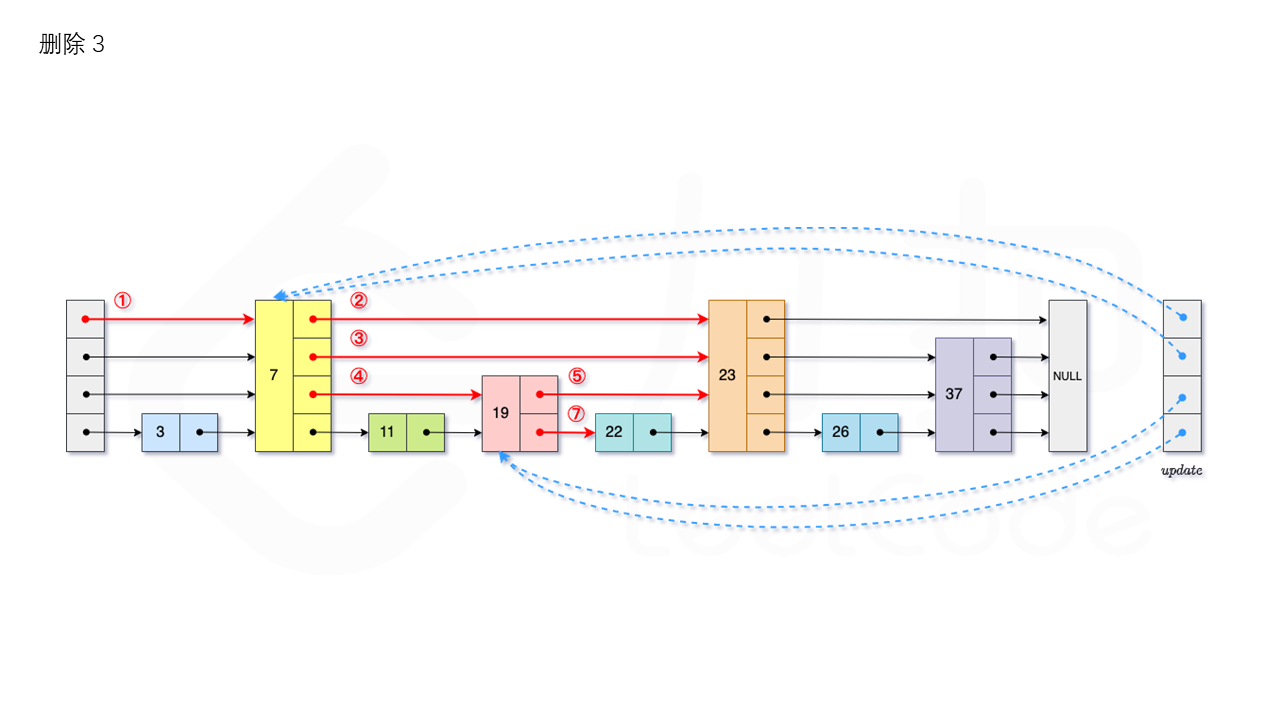
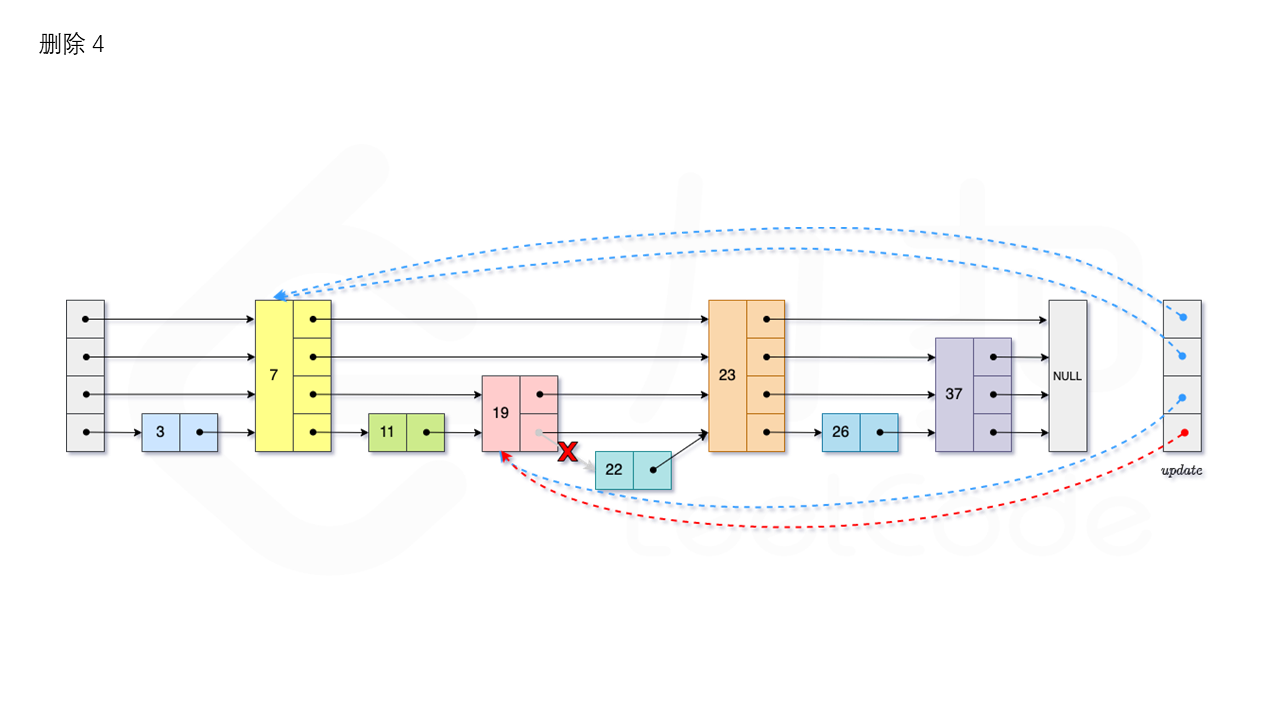
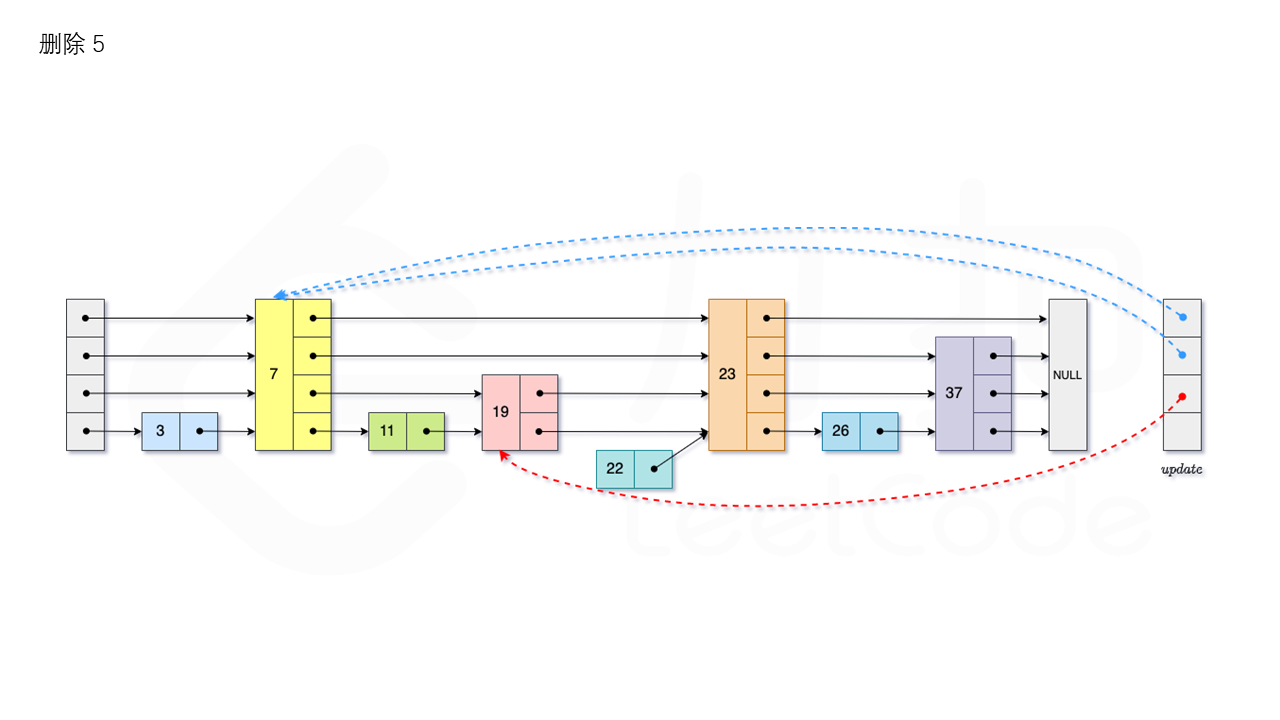
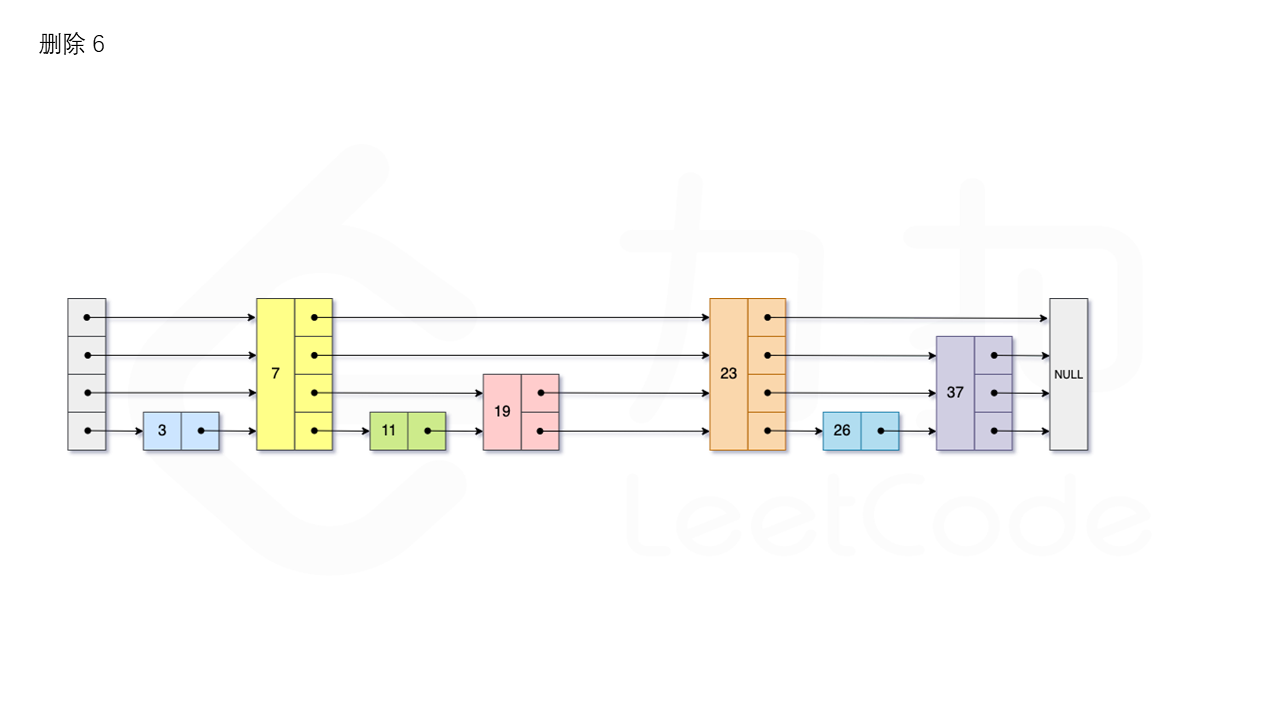
1.3.3 删除

首先我们需要查找当前元素是否存在跳表中。从跳表的当前的最大层数 level 层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第 1 层。如果第 1 层的下一个节点不等于 num 时，则表示当前元素不存在直接返回。我们用数组 update 保存每一层查找的最后一个节点，第 i 层最后的节点为 update[i]。此时第 i 层的下一个节点的值为 num，则我们需要将其从跳表中将其删除。由于第 i 层的以 p 的概率出现在第 i+1 层，因此我们应当从第 1 层开始往上进行更新，将 num 从 update[i] 的下一跳中删除，同时更新 update[i] 的后续节点，直到当前层的链表中没有出现 num 的节点为止。最后我们还需要更新跳表中当前的最大层数 level。如图所示：